INTRODUCTION
In early October, a Scope Out Next Month reader asked me to “photo the nearest star, and tell us about it.” The Alpha Centauri system of three gravitationally bound stars is actually the our closest stellar neighbor at about four light-years away. A telescope is required to discern the two dimmer components Alpha Centauri B and C. Alpha Centuari A, however, is similar to our Sun in size, mass and spectral family, and appears to us as the third-brightest star in all of the Earth’s night sky. This star is located sufficiently deep in the southern hemisphere sky that it is perpetually hidden from view at from my northern location of 39° north. In order to account for the closest star that I could photograph, I qualified the question with “visible from my northern hemisphere location” and the star that I seek becomes Barnard’s Star, our fourth closest stellar neighbor after the three stars of the Alpha Centauri system. This star is quite unlike our Sun. It is a low-mass red dwarf that even at about six light years away is too dim to be seen with the naked eye. An interesting characteristic of this star is that it has the highest proper motion against the “fixed” background stars of any star that can be observed from Earth. As I will describe later, the reader’s question is not the beginning of my journey to Barnard’s Star.
I did my homework (planning) and managed to get out on a clear night to capture a photograph that included Barnard’s Star. I have since written up a description of this object and posted it and the photograph to Jim Johnson’s Astronomy Web site. The reader next tells me that it boggles his mind that I can find a specific star out of all of those billions. I started writing a quick response to unboggle (unbottle?) his mind, but the scope of this response soon grew much more involved than I had anticipated. I eventually abandoned the email in favor of this essay-length piece that I could more widely share by posting to my Web site. This article is about the principles, planning and techniques that I used to find Barnard’s Star.
To define the problem, let’s first examine two easy techniques to find a celestial object. If I were looking for a bright naked-eye object, such as the Moon, Jupiter, or Saturn, finding it and photographing it would be quite simple. I simply point the telescope at the object by aiming the telescope’s red dot finder at the object, and the object, which I can clearly see without the telescope, can also be seen within the eyepiece field of view with little if any additional adjustment of the telescope. There is also an easy way to find objects that cannot be seen with the naked eye. A computer-driven GOTO telescope mount can be commanded to drive the telescope to the object’s coordinates, and GOTO capabilities are within reach of amateur astronomers with very modest telescopes. But alas, Barnard’s Star is too dim to see with the naked eye, and I do not have a GOTO mount! Let’s explore how else I can point the telescope at an object that is too dim to see and is hidden among so many other stars.
Let’s begin with a discussion about what can and cannot be seen either with an unaided eye, a telescope, or a photographic exposure. The two primary factors are the brightness (or darkness) of the sky compared to the brightness (or dimness) of the object, which is essentially a signal-to-noise ratio proposition. Objects (signal) that are dim will be increasingly lost in the background as the sky (noise) becomes brighter. This is why astronomers crave dark skies! The apparent brightness of a star as seen from Earth is measured on a magnitude scale. For example, Vega, a very bright star in The Summer Triangle, is a 1st magnitude star. Brighter stars have lower magnitudes and even go in to negative magnitudes, and dimmer stars have higher magnitudes. A 6th magnitude star is about the dimmest star that we can see in a completely dark sky. In a light-polluted urban setting, a 4th magnitude star might be the limit, and perhaps 3rd magnitude becomes the limit if the full moon is above that urban horizon. Barnard’s Star is a 9.6 magnitude object, so I am not able to observe it directly. This is where the light gathering ability of a binocular or a telescope comes in. At some point for a given telescope’s optics, long-duration photographic exposure is required to detect very dim objects.
There are a few guiding principles to keep in mind in finding an object like Barnard’s Star that cannot be seen with the unaided eye. First start with brighter things that can be seen with the unaided eye, and work down toward increasingly dimmer objects that can be seen at the eyepiece and then things that can only be seen in a long-duration photographic exposure.
The next principle is to start at a wide field of view. As the desired star field is identified and centered up at each stage, proceed by increasing magnification, which also has the effect of narrowing the field of view and bringing increasingly dim stars into view.
And the final principle is that it is important to select the correct magnitude of stars displayed in each chart so that the charted stars match what is seen with the unaided eye (wide view/5th magnitude and brighter), at the eyepiece (medium view/10th magnitude and brighter) and in the image (close view/14th magnitude and brighter). As extreme examples, including stars down to 14th magnitude in the wide field chart would overwhelm the chart with thousands upon thousands of stars, and selecting only down to 5th magnitude stars in the close field of view chart would yield a chart with just one star. Neither chart would be useful in our quest for Barnard’s Star.
PLANNING
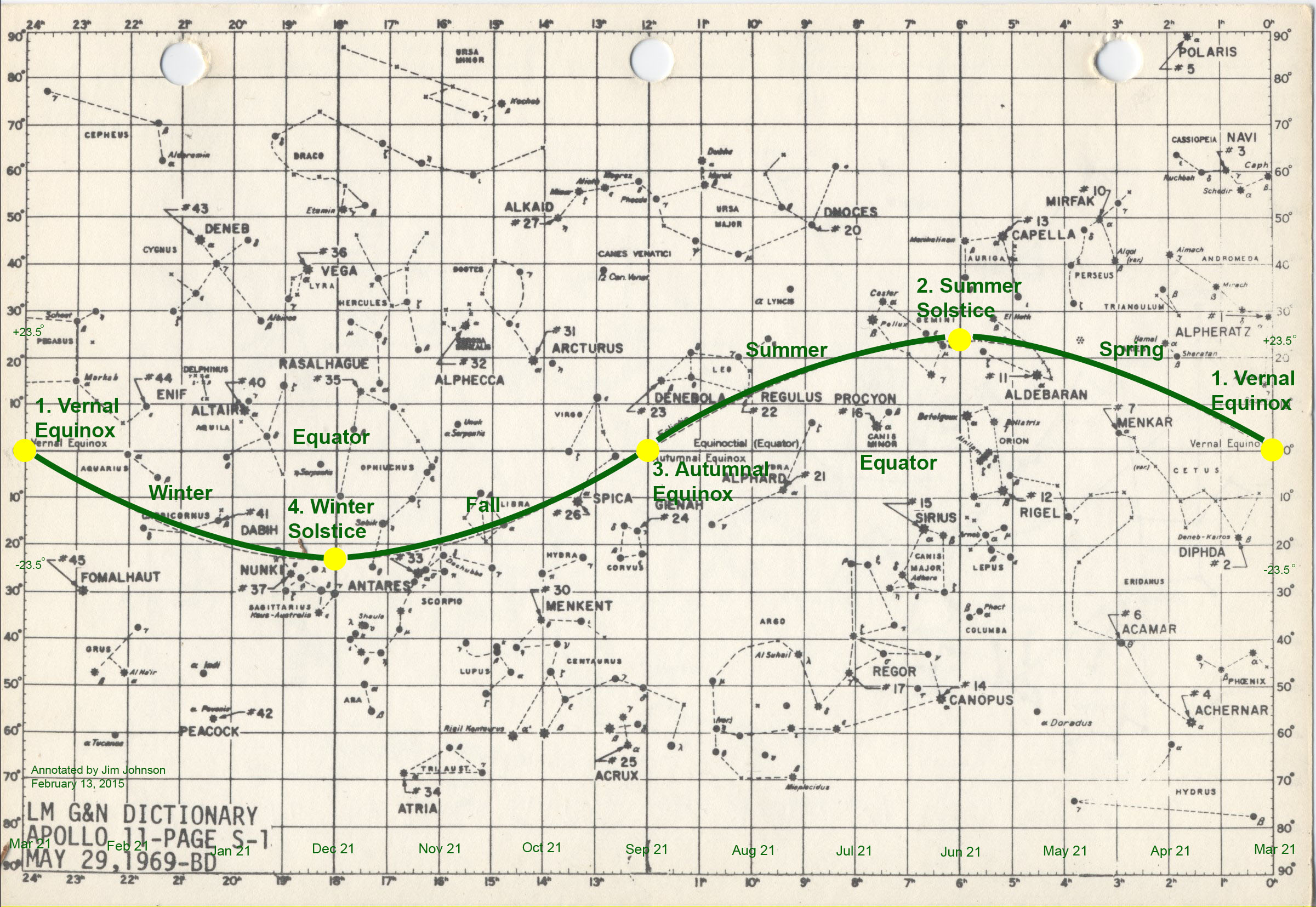
At the planning stage, I am indoors, and at the computer. The first step, is to identify the constellation in which the target is located, and where the target is within that constellation. I also want to know the target star’s right ascension and declination, which is the sky’s rough equivalent to the latitude and longitude on the Earth’s surface, so that I can precisely locate the target in a star chart. I find this information in Wikipedia and make a note that Barnard’s Star is located in the constellation Ophiuchus at 17 hours, 57 minutes and 49 seconds of right ascension, and +4 degrees, 41 minutes and 36 seconds declination. For my immediate purpose , Ra 17h58m/Dec +4d42m is quite close enough. Plus 4 degrees, by the way, means four degrees north of the celestial equator.
I take the right ascension and declination information to Cartes du Ciel, the freeware charting software that I use, and note that Barnard’s Star is located in the northeastern part of the constellation Ophiuchus. In order to complete this exercise, I need to prepare three charts that are centered on Barnard’s Star’s location. The first one is a wide-field, constellation-level chart that will help me point the telescope to the right part of the sky. The stars in this chart are of roughly the same magnitude as those that can be seen with the unaided eye. Narrowing down the field of view a little more, a medium field of view chart will help identify the stars that can be seen at the telescope eyepiece. And finally, a narrow field of view chart will be needed to see even dimmer stars, which provide the context needed to positively identify the target star in a long-duration photographic exposure.
The final step in planning is to determine if Barnard’s Star’s constellation, Ophiuchus, can be viewed in the sky on the date and at the time that I wish to attempt a photograph, or 7pm in mid-October in this exercise. This step is necessary because the time of day and the time of year determines whether the desired constellation is visible in the sky, or where it is in the sky. Why? Because any object or any given set of right ascension/declination coordinates does essentially what the sun does, it makes approximately one revolution about Polaris each day due to the Earth’s rotation. Holding the time of day constant and stepping through a year’s worth of days, an object or set of coordinates makes one rotation about Polaris in a year due to the Earth’s orbit about the Sun.
To illustrate the annual rotation, lets follow Ophiuchus over the course of a year. In October it is visible in the western sky in the evening after sunset, and due to the Earth’s daily rotation about its axis, it too sets below the horizon about four hours after the sun does. Each evening, the progression of the Earth’s orbit about the sun causes Ophiuchus to appear just a little closer to the sun than it did the evening before, and the interval between sunset and Ophiuchus setting below the horizon gets almost imperceptibly shorter from one evening to the next. Two months later in December, Ophiuchus has already set below the horizon before it is dark enough to see its stars. Between December and January, the Sun is located near the star field represented by Ophiuchus, and rendering it completely impossible to see this constellation at any time during the day. By January, Ophiuchus can be seen again as it emerges from behind the sun, and rises in the east just before sunrise. Each morning, it rises just a little earlier, and by May it rises in the east just after sunset, which means that it is easily seen in the early evening. And finally, by October it is once again visible in the west as soon as it is dark enough to be seen.
To complete this final planning step, I set a planosphere for 7pm in October, and I could also see that Ophiuchus was above the horizon in the west. With an observation plan in hand, and having ascertained that the target will be well-placed in the sky, I begin monitoring my observatory’s Clear Sky Chart to find a suitable evening to set up the telescope and execute my plan.
FINDING
A clear evening finally arrives, so it is now time to begin working outdoors at the telescope. To follow along, first open and examine the wide field chart, which charts the stars that I can expect to see with my unaided eye. Since I cannot see Barnard’s Star directly, I will have to work with what I can see to help me point the telescope toward the star field where Barnard’s Star is located. First, examine the wide field chart to become familiar with the constellation and the location of Barnard’s Star therein. The red circle and rectangle near the center of the image are centered on Barnard’s Star, even though this particular star is not bright enough to appear on this chart. Note the right ascension and declination coordinates on the bottom and left edges of the chart, and that the circle and rectangle are indeed centered on the coordinates that I looked up earlier on Wikipedia. The circle represents the field of view of the Panoptic 35mm eyepiece that I intend to use to directly view the star field, and the rectangle represents the field of view of the Canon EOS 60Da camera with which I will capture images. Also note in the upper left corner of the image that stars of magnitude 5 and brighter are displayed, and that the field of view is almost 180 degrees, or essentially the whole visible sky.
With this sense of scale to help me determine where to point the telescope, I proceed by devising a star hopping strategy. I select Beta Ophiuchus as my visual jumping off point to Barnard’s Star, and since this star is not easily confirmed in my light-polluted back yard, I first locate the brightest, closest, most easily identified object that I can find, The Summer Triangle. In the chart, the Triangle stars, connected by my light colored triangle annnotation, are Alpha Lyra (Vega), Alpha Cygnus (Deneb), and Alpha Aguila (Altair). I first hop from Altair and Vega via the red lines to Alpha Ophiuchus, the brighest star in that constellation and then down to Beta Ophiuchus, the second brightest star and my jumping off point for arriving in the vicinity of Barnard’s Star. I then find all of these stars in the sky, eyeball the scale and distance, and place the telescope’s red dot finder to the point in the sky just to the left of Beta Ophiuchus.
To follow at this stage, open the medium-field of view chart and examine it. There are a few things to note here. First, the magnitude in this chart is increased to display stars down to magnitude 10.3 and brighter, there are now stars visible within the circle and rectangle, and the circle and rectangle appear much larger as the field of view has narrowed from 180 degrees down to 11 degrees. Second, I note the two most distinct objects in the chart: the sharks nose (my naming) asterism of stars that I connected with red line segments in the upper left of the rectangle, and Ophiuchus 66 in the lower left of the rectangle. If I can bring the the shark’s nose and Ophiuchus 66, which is much brighter than anything near it, into the eyepiece field of view, then Barnard’s Star (white carat) must also be in the field of view. The implication of this fact meant that I did not need to positively identify Barnard’s Star while I was a viewing at the eyepiece. I could, however, see what I thought to be Barnard’s Star, but the dimmer stars needed to confirm this sighting were not visible in the eyepiece.
It is time to locate the desired star field in the eyepiece and capture an image. The wider field of view of the eyepiece compared to the camera’s field of view, and the fact that I can see the star field move in the eyepiece in real time as I search for the correct star field helps me locate the correct star field much faster. On the night that the image was captured, I was fortunate to find the shark’s nose asterism and Ophiuchus 66 with only minor moving around once I pointed the red dot finder just to the left of Beta Ophiuchus. Next, I centered up my intermediate targets in the eyepiece, and swapped out the eyepiece for the camera at the telescope’s rear aperature and refocused. I snapped a single 25-second image, and voila, I could see the asterism and Ophiuchus 66 in the camera’s rear display. Open the actual full frame image that I captured and do a side-by-side comparison with the medium field of view chart. Also note that the orientation of the full frame image and the frame in the medium field of view chart are not the same. It was not important that the camera frame have the same orientation as the chart, because my mission in life at this point was simply to capture the shark’s nose and Ophiuchus 66 in the same frame.
ANALYSIS
I am back indoors at the computer, and not necessarily on the same night, to perform the analysis that will confirm that I found Barnard’s Star. To follow along at this stage, open the close field of view chart. Note that it display stars all the way down to magnitude 14.2, and many more stars are visible. The field of view, which is now only about 1 1/2 degrees (compared to the original 180 degree field of view), is completely inside of the camera’s rectangular field of view as noted by the rectangle in the previous chart. Ophiuchus 66 can be seen way down in the lower left corner, and I connected the shark’s nose stars with a white dotted line. In order to positively identify Barnard’s star, which is annotated, I first matched the brighter stars in the chart with those in the in the image. I used a red line in the image to mark a star hopping path from the tip of the shark’s nose through the dimmer stars down to Barnard’s Star, and I highlighted a wishbone asterism that caught my eye in some online images of Barnard’s Star. Open the cropped image of the star field and do a side-by-side comparison with the image of the close field chart, and see if you can star hop from the tip of the shark’s nose to Barnard’s Star in the cropped image. For extra credit, devise an alternate star hopping path and reconfirm the result, or even repeat this exercise in any Barnard’s Star image that you find online.
CLOSING
I feel a great sense of accomplishment in finding and photographing this star, and it pleases me greatly to share my work. I should share with you that this exercise was slightly over-simplified, because no transformation is required to equate the chart view to the images captured by the camera. At the eyepiece, a star field may be flipped horizontally, vertically or in both directions, depending upon the type of telescope (reflector or refractor) and whether a 90-degree prism is in the optical path determines whether transformation is required. If needed, the chart can be set to display the stars as they will be seen in the eyepiece by flipping the chart horizontally, vertically, or in both directions to match the eyepiece view.
So what’s next? I have known since childhood that Barnard’s Star has the fastest proper motion of any star that we can see from Earth, and I have dreamt of demonstrating this motion for myself for as long as I have known this fact. Sure, I can look at existing images of the star field that have been taken during my lifetime, and plot its motion. But now that I have captured my own baseline image, I need only capture another image at some point in the sufficiently distant future and note that its location has shifted from the baseline image, and I will have demonstrated this motion for myself! The optics/sensor combination that I used in October equates to about 1.6 arcseconds per pixel, and Barnard’s Star’s movement of 10.3 arcseconds/per year should result in about six pixels of movement relative to the background stars. I will take a second photograph in a year, and attempt to detect Barnard’s Star’s movement, and report back my finding.
An interesting consequence of Barnard’s Star being so close to us is that it has a very high parallax shift against the “fixed” background stars as the Earth moves from one side of the Sun to the other in a six-month, or half-orbit period. To demonstrate parallax shift, hold a pencil point out at arm’s length, close one eye and note the point’s position against the more distant background. Without moving the pencil, view the pencil point with the other eye open, and close the first eye. Note how the point shifts against the background. Before six months from October rolls around, I will be doing some analysis to determine if it is possible for me to detect Barnard’s parallax shift against the background stars in April when the Earth has moved around to the other side of the Sun. The distance between the two observation points, which is analogous to the distance between one’s eyes in the pencil illustration, is roughly 193-million miles. If it is mathematically possible with my telescope/sensor combination, I will attempt to detect Barnard’s parallax shift and report back.
As a bonus, this exercise has demonstrated that imaging Pluto is within my reach! The prospect of producing my own images of Pluto (still a planet in my mind, logical arguments for why Pluto is or isn’t a planet notwithstanding!) also captured my imagination in grade school when I saw first saw Clyde Tombaugh’s pair of images taken on the nights of the 23rd and 29th of January in 1931. Next July 4th, when Pluto and Earth are at their closest approach for 2015, Pluto’s angular velocity will be about 1 1/2 arcminutes per day, which is almost 200,000 times faster than Barnard’s Star’s motion (10.3 arcseconds) against the background stars! This means that I can detect Pluto’s motion by taking images just a few days apart instead a year apart. Pluto’s magnitude will be about 14.1, which is brighter than some of the stars that are visible in my Barnard’s Star image. I can improve my chances of detecting Pluto by exposing just a little longer, and by stacking multiple images to reduce background noise.
© 2014 James R. Johnson
jim@jrjohnson.net