Магазин ОМГ онион
Правильная ссылка на ОМГ онион в обход блокировки РоскомНадзора в обход блокировки через тор и обычный браузер. Рабочий список зеркал OMG union. Вход на форум сайта OMG com.
Ссылка на сайт OMG в клир – omgomg.store
Актуальный вход форума OMG onion
Найти нужную страницу. Если у Вас нет Yandex или Google в списке, значит сайт ОМГ, Вы должны были добавить через обычный поисковик, но Вы ошиблись при вводе адреса сайта. При вводе адреса сайта, Вы вводили адрес в строку поиска Yandex или Google. С появлением интернета в жизни пользователя, возникает необходимость в работе в интернете. В интернете можно купить абсолютно все. Начиная, от книг, заканчивая компьютерами, одеждой, телефонами, автомобилями и недвижимостью.«вход на ОМГ». После чего вы попадете на главную страницу главной страницы, на которой и находится ссылка на OMG onion. У сайта OMG есть два основных зеркала: ссылка на ОМГ в торе и ссылка на ОМГ onion. Первое из них является главным зеркалом сайта, а второе зеркало сайта ОМГ. Если Вы из Москвы, то можете воспользоваться ссылкой на OMG. Чтобы попасть на ОМГ через браузер, для этого достаточно иметь только доступ в Интернет, а также знать ссылку на сайт магазина OMG.
ОМГ является одним из самых безопасных и надежных сервисов. Многие пользователи предпочитают использовать именно его, т.к. он защищен от взлома. А, как известно, злоумышленники пользуются подобными инструментами для отмывания и вывода средств. В сети существуют аналоги ресурса, но их безопасность и удобство оставляет желать лучшего. За счет этого, многие клиенты предпочитают именно сайт ОМГ, где можно безопасно оформить заказ, и получить товар за считанные минуты.ОМГ представляет собой веб-ресурс с уникальным функционалом, позволяющий пользователям безопасно купить товар или заказать услугу. Данный ресурс создан для всех категорий людей: покупателей, продавцов и других пользователей. ОМГ – это сайт, который позволяет пользователям безопасно приобретать товар или заказывать услуги с уникальным функционалом, который позволяет клиентам совершать покупку не находясь в сети. ОМГ предлагает широкий ассортимент товаров и услуг.
Как зайти через браузер тор на сайт ОМГ ссылка ссылка на ОМГ в тор браузер скачать OMG onion. OMG onion – криптомаркет нового поколения, работает на огромной. Ссылка на ОМГ в тор браузер скачать – bobfilm. На ОМГ продаётся и продаётся. OMG onion – криптомаркет нового поколения, на данный момент плотно. OMG onion – криптомаркет нового поколения, работает на огромной. Ссылка на ОМГ в тор браузер скачать (Москва) Ссылка на ОМГ в тор браузер скачать (Москва)На первый взгляд кажется, но для этого следует узнать, это необходимо для того, что не все они надежные. Чтобы обезопасить себя, что за ними стоит одна и та же организация с одинаковыми адресами, чтобы узнать, на сегодняшний день многие люди ищут в интернете возможность заработка. Все происходит в режиме онлайн. В-третьих, где можно узнать о том, как зайти на зеркало ОМГ. ОМГ один из самых популярных и посещаемых ресурсов в сети. Но при этом многие из них не являются полностью безопасными.
Зеркала ОМГ работают по следующей схеме – Вы заходите под своей основной учетной записью на сайте. После этого Вы получаете ссылку для перехода на сайт ОМГ. Вы заходите на зеркало сайта и переходите к загрузке приложения для iOS. После этого приложение автоматически соединяется с сетью TOR и выдает вам в результате список ссылок, переход по которым может вывести Вас на сайт ОМГ Сайт ОМГ – это https:OMG.onion/ магазин моментальных покупок в tor, который действует по СНГ.На нём вы найдете зеркала для браузеров Google Chrome и Mozilla, а также плагин, который позволяет зайти на ОМГ, минуя любые блокировки. Если вам нужна ссылка на «ОМГ», можете посмотреть ее и скопировать. При этом вам не нужно ничего скачивать или устанавливать, просто скопируйте и вставьте в адресную строку. Зеркало для Chrome и Firefox. Зеркало для Opera. Если у вас сайт открылся, но выдает ошибку, то нажмите кнопку «Открыть» над окном браузера, и оно откроется в новой вкладке.
ОМГ зеркало: https:OMG.com Вы можете использовать его так же, как и оригинальный сайт. На зеркало идут только ссылки и, естественно, они тоже будут работать. Также на зеркало можно попасть через любой браузер в специальном домене. Вы попадете на сайт из зоны.onion, поэтому на него не ведется никаких технических атак. На OMG вы можете купить товар из любой страны мира. У ОМГ есть множество международных способов доставки и оплаты. Вы можете выбрать любой удобный для вас способ.Все сайты, зеркала и т.д. находятся в общем пространстве, а не в разных странах или на разных серверах. Ссылку на вход в ваш личный кабинет вы можете найти на нашей странице “Контакты”. Помните, что вход в систему возможен только с использованием логина, пароля и адреса электронной почты, которые указывали при регистрации (при условии, что регистрация была правильной). Если логин или пароль не подходят, то, скорее всего, вы не ввели их правильно при регистрации.
Основное зеркало ОМГ в онион даркнет
На сегодняшний день существуют несколько сайтов, на которых осуществляется продажа недвижимости. Многие из них предлагают жильё в новостройках, а также вторичное жильё. Кроме того, на этих сайтах Вы сможете найти различные варианты по аренде жилья. На таких сайтах обычно размещают объявления о продаже недвижимости, которые не привязаны к конкретным людям. В то же время данные объявления могут быть привязаны к конкретным людям, которые на данный момент времени проживают в этом жилье.Тем более что сегодня можно расплачиваться непосредственно с помощью Яндекс.Денег. Для этого следует войти в личный кабинет сервиса и выбрать пункт «Перевести». На экране появится окошко, в котором потребуется указать номер карты Сбербанка и сумму перевода. Далее остаётся подтвердить операцию. Это можно сделать с помощью кода, который будет выслан на указанный мобильный телефон. После этой процедуры деньги придут на карточку Сбербанка, и на экране пользователь увидит оповещение.
Все данные, которые пользователь указывает для авторизации, сохраняются абсолютно в безопасности. У вас не пропадет возможность пользоваться услугами сайта, так как оно является точной копией оригинала, которую можно открывать не только с компьютера, но и с любого мобильного устройств. Но это не единственное, в чем плюсы данного сайта. Благодаря тому, что ресурс постоянно работает над оптимизацией и расширением своего функционала, его посещают миллионы пользователей каждый день.И если вы не можете зайти на основной сайт по какой-то причине, то попробуйте использовать зеркало. Если вы зашли на сайт через зеркало, то вы увидите, что он точно такой же, как и главный сайт. У вас будет доступ к тем же функциям, что и на главном сайте. Поэтому это не влияет на работоспособность сайта. Зеркало ОМГ — это сайт, который полностью повторяет функционал и дизайн основного сайта OMG. Все товары и услуги на сайте полностью идентичны с главной сайта.
Зайти на сайт ОМГ можно не только с компьютера, ссылка на ОМГ, Как зайти на ОМГ через тор. ОМГ ссылка для обычных браузеров: Зеркало для браузера Тор: hq OMG как зайти на сайт OMG и зеркала: OMG Onion. OMG onion – криптомаркет нового поколения, работает на огромной территории всем OMG onion OMG на стран СНГ. На данный момент орудует огромное количество мошенников, это дипвеб торговая площадка, все,Это абсолютно бесплатно и безопасно! Если сайт заблокирован, на помощь придет Тор Браузер, с его помощью можно заходить на заблокированные сайты и любимые онион сайты. Tor Browser работает так же, как и любой другой веб-браузер (программа, используемая для просмотра веб-сайтов, например Chrome, Firefox или Safari). Он способен в разы сократить расстояние между вашим интернет-браузером и. Как зайти на сайт ОМГ в обход блокировки – моментальная площадка по продаже товаров по всей России.
Помимо этого, через прокси-сервис можно не только заходить в личный кабинет, но и осуществлять вход в личный кабинет, при этом не нужно будет вводить логин и пароль. Это делает работу в личном кабинете максимально безопасной. На сегодняшний день в личном кабинете «Мои достижения» содержатся следующие вкладки: «Достижения» (вкладка доступна после авторизации в личном кабинете); «Мои достижения» — по сути, это каталог, в котором собраны все ваши сертификаты и свидетельства, а также дипломы;Все указанные сайты предлагают возможность получить бездепозитный бонус за регистрацию. Все перечисленные и многие другие бонусы, также доступные для Кеш-бонуса, предоставляются исключительно в валюте игрового счета — рублях В большинстве интернет-казино, принимающих депозиты в рублях, есть возможность для получения бонуса на первый депозит. Кроме этого, с помощью бонусов вы можете получить дополнительные деньги и свободные спины для игры в рулетку или другие игры казино.
Другие же имеют свои недостатки и неудобства. Ниже мы рассмотрим их подробнее. ✦ Зеркало. Это сайт, который имеет внешнее отличие от оригинального сайта OMG. Он работает точно так же как и OMG, но только в зеркальном отражении. Таким образом, браузер TOR будет использовать для вас только проверенный сайт, а вам придется посещать только проверенный сайт зеркал.Мы используем обычные зеркала, а также зеркала, которые предоставляют сами пользователи. Сейчас мы постараемся рассказать об этом подробнее. Обычные зеркала сайтов. Это специальные сайты, которые являются клонами основного сайта. По сути, это копии сайта, которые могут быть не связаны с оригиналом. Такие зеркала предлагают, как правило, только доступ к основному сайту. На них не бывает рекламы, и никто не может запретить вам скачивать, смотреть или даже пользоваться другими услугами.
Перевести деньги на сайт ОМГ в онион
Ссылка на ОМГ ОМГ – https OMG onion biz официальный сайт, официальный сайт представляет собой огромную площадку в интернете, А что за OMG onion в россии отзывы для «ОМГ»? Это ОМГ сайт, onion. На котором можно купить любой товар. Здесь сразу – адрес сайта ОМГ онион нет, OMG onion – криптомаркет нового поколения, работает на https OMG onion biz официальный сайт огромной территории всего бывшего Союза, По словам разработчиков, сайт полностью.— всегда есть резервный сайт, https OMG com в обход блокировки это такой же популярный сайт, как и основной ресурс. Как зайти на сайт ОМГ с айфона OMG представляет особой один из самых крупных маркетплейсов в России и странах СНГ на сегодняшний день. На просторах этой интернет-площадки каждый пользователь может приобрести товар или услугу, которая находится за гранью закона. В связи с блокировкой ресурса у сайта ОМГ периодически обновляются зеркала для её обхода.
Именно это и является его главным достоинством. В частности, не нужно искать, где находится торговая площадка, поскольку ОМГ – это всегда актуальное зеркало. К тому же, пользователь может не беспокоиться о сохранности средств, так как они хранятся на официальном сайте компании. Также стоит отметить, что ОМГ – это всегда надежные и безопасные товары, которые доступны для покупки. На ресурсе не удастся найти подделки, а также некачественный товар. Это позволяет не сомневаться в его качестве.Помимо этого, данный веб-ресурс предоставляет широкий выбор, благодаря чему пользователь может подобрать товар по вкусу и по карману. На сайте имеется удобная поисковая система, позволяющая с легкостью отыскать нужный товар. Помимо этого, на сайте представлены многочисленные категории, которые облегчают поиск продукции. В каталоге магазина, имеются товары разных категорий, что позволяет клиенту отыскать продукцию, соответствующую его требованиям.
Http OMG vc com. OMG сайт анонимных email, OMG зеркало мобильная версия. ОМГ магазин моментальных покупок прямая ссылка. OMG onion market 469! OMG onion images momental public. OMG fm официальное зеркало ОМГ Официальный шлюз от команды OMG анонимность и самая высокая скорость загрузки гарантирована. Ссылка на ОМГ OMG union зеркала. OMG не робот 1 в 1 с оригинальной. OMG onion отзывы что. OMG зеркала ссылки.Скачать ОМГ tor. Ссылки на сайт. Ссылка на ОМГ скачать на. OMG onion ссылка. OMG onion ссылка. OMG onion ссылка. OMG onion ссылка. OMG onion ссылка. OMG OMG onion torrent magnet отзывы. OMG onion ссылка. OMG onion ссылка. OMG onion ссылка. OMG onion ссылка. OMG onion ссылка. OMG onion ссылка. OMG onion ссылка. OMG onion ссылка. OMG onion ссылка. OMG onion ссылка.
Вы можете попробовать найти актуальное зеркало с помощью одного из наших адресов. Зеркало сайта «ОМГ», как и официальный сайт, всегда доступны с помощью нашего сервиса. По этой причине мы советуем вам использовать для входа в «ОМГ» браузер Тор. Он скрывает вашу личность и защищает вас от. Вход на «ОМГ через TOR» Далее ссылки, чтобы скачать Tor Browser. ГДЕ БРАТЬ ДЕНЬГИ В ТОРРЕНТЕ При этом ссылки на ОМГ вы можете найти в Telegram, который отличается повышенной надежностью.Однако этот пробел можно устранить — с помощью бота, который работает на автомате. Для этого достаточно ввести команду в консоль, и бот найдет и скачает зеркало, которое больше нигде не указано, но на которое при этом заходит большинство пользователей. После этого можно заходить на сайт через зеркало, которое автоматически будет открываться в браузере. На ОМГ возникают сложности с поиском зеркала, особенно если вы входите в сеть с нескольких компьютеров или мобильных устройств.
После выбора страны можно указать номер телефона, на который придет SMS с кодом для подтверждения. Бонус на первый депозит. На официальном сайте 1хбет есть раздел 1xGames с различными играми. Служба безопасности 1xBet может запросить документы для подтверждения личности и проведения денежных операция. 1xbet-зеркало рабочее на сегодня прямо сейчас Для начала работы необходимо авторизироваться. Вывод средств возможен на тот же счет, с которого игрок пополнял свой баланс.На сегодняшний день существует множество способов для обхода блокировки интернет ресурсов, например: 1. Использование VPN (Virtual Private Network) сервисов. Для этого необходимо установить программу на свой компьютер, с ее помощью будет происходить перенаправление трафика и создание новой сети. 2. Онлайн анонимайзеры. Принцип их работы заключается в использовании ресурсов всемирной паутины для сокрытия своего настоящего IP адреса. 3. Использование браузера Tor.
Сайт OMG com для входа в магазин OMG
Чтобы зайти на ОМГ, вам нужно установить специальный браузер на своем компьютере. Для этого скачайте Tor Browser по ссылке в статье. После установки вам нужно будет ввести свой номер телефона и нажать «Получить код». На него вам придет смс с кодом, с помощью которого вы сможете войти в приложение. После этого, на вашем устройстве будет находиться зашифрованное соединение между вами и сайтом. Вы точно так же вводите данные в браузер и заходите на ОМГ.Это позволит вам получать доступ к сервисам ОМГ, не опасаясь слежки и блокировки. В настоящий момент, вы можете войти на сайт ОМГ через наше новое зеркало. Что нам потребуется для успешного входа на сайт ОМГ? Для входа на сайт вы можете использовать любой браузер, если вы знаете как это сделать, то вы можете узнать, перейдя по ссылке. Если у вас есть доступ к сети Tor, вы можете использовать его для входа на сайт, но не будем останавливаться на этой детали.
ОМГ онион ссылка на тор на русском OMG ru onion browser. ОМГ магазин онион 0 на. Обход блокировки сайта OMG за 5 минут, а так же рабочая ссылка ОМГ Именно столько времени займет настройка и установка Тор. Сайт OMG OMG onion в россии скачать бесплатно тор браузер официальный сайт ОМГ. VPN, Tor и прочие анонимайзеры – все о безопасности ОМГ онион ссылка тор на русском. Также не забываем оставлять отзывы о товарах после покупки!и Вы попадете на наш сайт. Ссылка на ОМГ в Тор браузере. OMG onion (ОМГ сайт, OMG,OMG center, OMGonion) это крупнейший криптомагазин запрещенных товаров и услуг который обслуживает пользователей всего СНГ. Как войти на OMG? Если не работает и не открывается официальный сайт OMG center, то скорей всего у вас не установлены или отключены последние версии дополнений для браузера. В этой статье мы расскажем как зайти на ОМГ через Tor — браузер который они якобы используют.
+7418182 Для Вас есть:  – ОМГ магазин моментальных покупок в обход блокировки. Зайти на OMG.union – OMG.union – магазин моментальных покупок в обход блокировки.
– ОМГ магазин моментальных покупок в обход блокировки. Зайти на OMG.union – OMG.union – магазин моментальных покупок в обход блокировки.  – OMG – как правильно добавлять сайт на закладки;
– OMG – как правильно добавлять сайт на закладки;  – гидроденьги.рф – рабочее зеркало ОМГ. Как зайти на ОМГ? Onion ссылка на OMG для Тор браузера: kripter.OMG-ru20.com Анонимность и скорость на. Как создать закладку в тор браузере попасть на ОМГ – что Как зайти на ОМГ?ОМГ сайт: https:OMG.onion/market/298
– гидроденьги.рф – рабочее зеркало ОМГ. Как зайти на ОМГ? Onion ссылка на OMG для Тор браузера: kripter.OMG-ru20.com Анонимность и скорость на. Как создать закладку в тор браузере попасть на ОМГ – что Как зайти на ОМГ?ОМГ сайт: https:OMG.onion/market/298 

 . ОМГ онион шоп – интернет магазин в сети tor. Магазин ОМГ shop работает по территории РФ, Беларусии, Украины. OMG – как попасть на ОМГ? https:hydrа2web.cоm/ — Ссылка для браузеров без Tor соединения ОМГ Однако, на мой взгляд, в таком виде – лучше. Все, что происходит на сайте и в приложении, остается в системе. Даже, если зайти на сайт напрямую с зеркала, то все равно можно будет определить зеркало.
. ОМГ онион шоп – интернет магазин в сети tor. Магазин ОМГ shop работает по территории РФ, Беларусии, Украины. OMG – как попасть на ОМГ? https:hydrа2web.cоm/ — Ссылка для браузеров без Tor соединения ОМГ Однако, на мой взгляд, в таком виде – лучше. Все, что происходит на сайте и в приложении, остается в системе. Даже, если зайти на сайт напрямую с зеркала, то все равно можно будет определить зеркало.
То нужно зайти в телеграм канал, или в чат на сайте. Но лучше на сайт. Там найдёте более свежую и актуальную информацию. Если не работает официальный сайт, где можно найти зеркала Как найти зеркала ОМГ Если не работает официальный сайт ОМГ, значит его заблокировали по тем или иным причинам. Поэтому, чтобы попасть на ресурс, достаточно найти работающий и доступный вход на сайт, который предлагает ссылка на ОМГ. Но лучше посетить сайт. Это официальный сайт.После введения нового закона, интернет-магазин в сети тор не работает, но сайт работает по обычному адресу. Зайти на сайт ОМГ, чтобы приобрести товар, можно по зеркалу. Оно является своего рода дублером главного интернет-ресурса, который заблокирован. Но как зайти на ОМГ в торе? Зайти на сайт ОМГ с телефона Перейти на ОМГ по ссылке на сайте. Можно ли зайти на официальный сайт ОМГ с телефона? Зайти на ОМГ через мобилу, используя любой браузер.
Или с помощью программы Тор. Ссылка на ОМГ на зеркало. ОМГ онион зеркала: ОМГ онион зеркала. ОМГ онион зеркала. Все что нужно – перейти по ссылке в тени. Официальный сайт ОМГ: ОМГ сайт – ссылка на ОМГ. Ссылочка https OMG. У нас на сайте предоставлена ОМГ ссылка на зеркало, OMG, Но это не так. Если вы не читали книгу, что ОМГ ядовиты. Не все знают, скорее всего, то обязательно прочтите эту ссылку. Что ОМГ – это чудовище из древнегреческих легенд, а теперь давайтеОМГ зеркало. Ссылка на ОМГ, Ссылка на ОМГ, Ссылка на ОМГ. ОМГ онион сайты зеркала. Onion ссылка на ОМГ. Ссылка на ОМГ. Onion ссылка на ОМГ. ОМГ зеркало. Ссылка на ОМГ. Ссылка на ОМГ. Onion ссылка на ОМГ. ОМГ онион сайты зеркала. Ссылка на ОМГ. Onion ссылка на ОМГ. Ссылка на ОМГ. Как и прежде, мы все также рады вам на OMG onion. ОМГ онион ОМГ сайт моментальных покупок в обход блокировки роскомзазор магазин товаров.
Ссылка ОМГ на магазин моментальных покупок в даркнете
ОМГ – OMG onion – моментальный магазин. OMG Onion — криптомаркет нового поколения, функционирует на огромной территории. OMG – как попасть на ОМГ? garant.OMGonion20.com Onion-ссылка на OMG для Тор-браузера: garant.OMGonion20.com Забросить. В целом, OMG является одной из самых больших и безопасных площадок в сети. Сайт работает на огромной территории всего бывшего Союза, а так же. Как в тор попасть на ОМГ – сообщение Как я был на приёме в Кремле. Войти Регистрация.Скачать тор браузер бесплатно на русском с официального сайта на. Tor Browser — бесплатный браузер, который поможет сохранить полную анонимность, защитив интернет-соединение от наблюдения. Официальный Tor Browser для Windows, чтобы бесплатно скачать последнюю версию. Тор браузер длЯ планшета вход на ОМГ OMG in the us OMG onion. Скачать тор браузер бесплатно на русском с официального сайта на компьютер, нужно установить программу – Tor Browser.
Последнее время на площадке много. Как пройти регистрацию и получить доступ к личному кабинету. Инструкция по регистрации и входу в личный кабинет OMG. OMG вход в личный кабинет – OMG вход в личный кабинет – OMG – как сделать. Как зайти на ОМГ? Onion ссылка на OMG для Тор-браузера: Как зайти на ОМГ? Да, каждый из вас может оказаться в подобной ситуации, нужно просто зайти на наш сайт и прочитать информацию о том, как зайти на ОМГ, и как попасть в магазин OMG. Но что делать.USDT, ETH и BTC. На территории России деятельность. На территории России деятельность всех онлайн-магазинов, которые специализируются на продаже наркотиков, должна быть прекращена. Такое решение принял Верховный суд РФ. Как обойти блокировку магазина? Обходим блокировки в один клик. Обход блокировки ОМГ – наиболее популярный вопрос. В интернете вам предложат множество вариантов, как можно обойти блокировку ОМГ. КАК ПРАВИЛЬНО ОБХОДИТЬ БЛОКИРОВКУ ОМГ ВХОД В OMG
Как работает ОМГ: Все зеркала ОМГ рабочие, но в разное время. Если вам нужно создать закладку, вбейте в гугл или яндекс адрес нужной страницы, по ней и откроется зеркало. На сегодняшний день ОМГ является одним из самых крупных легальных магазинов товаров в сети. Как зайти на OMG: На данный момент вы можете зайти на OMG с любого устройства через ТОР. Для входа на ОМГ, вы можете скачать браузер ТОР. Скачать браузер ТОР можно по ссылке.но в большинстве случаев это не является причиной использования ОМГ через зеркала. Зеркало ОМГ работает по следующему принципу: у сайта ОМГ есть зеркало. Что такое зеркало сайта На самом деле это так. В связи с вступившим в силу запретом на анонимность в интернете, многие сервисы предоставляют доступ только через VPN, TOR или на свой страх и риск. Поэтому, чтобы зайти на любую страницу в интернете и не попасться на удочку мошенников, нужно скачать и установить ТОР-браузер.
OMG сайт для обхода блокировки — роскомнадзора и официального зеркала магазина. OMG сайт ссылка. Официальный шлюз от команды OMG, анонимность и самая высокая скорость загрузки гарантирована. Ссылка на ОМГ через TOR! Что такое ОМГ Сайт OMG. Тор ОМГ ссылка через тор на ОМГ сайт и. Как зайти на сайт OMG – Tor browser скачать бесплатно на iphone hyrda. При этом они получают возможность использовать систему в мошеннических целях.СКАЧАТЬ CLEARPLAY для OMG Ссылка на OMG в ТОР: https:cloud.mail.ru/public/3wZC/aM6c4WvzS  CLEARPLAY ДЛЯ OMG СКАЧАТЬ БЕСПЛАТНО: https:cloud.mail.ru/public/5b8a/m2hV5wyV2
CLEARPLAY ДЛЯ OMG СКАЧАТЬ БЕСПЛАТНО: https:cloud.mail.ru/public/5b8a/m2hV5wyV2  ССЫЛКА НА OMG ДЛЯ TOR БРАУЗЕРА: https:OMG.onion/market/1243
ССЫЛКА НА OMG ДЛЯ TOR БРАУЗЕРА: https:OMG.onion/market/1243  Как пополнить баланс на OMG: https:www.youtube.com/watch?v=gYHtCjV_iT4
Как пополнить баланс на OMG: https:www.youtube.com/watch?v=gYHtCjV_iT4  КАК ПОПОЛНИТЬ БАЛАНС НА OMG: https:www.youtube.com/watch?v=l-e8wzTpkKc
КАК ПОПОЛНИТЬ БАЛАНС НА OMG: https:www.youtube.com/watch?v=l-e8wzTpkKc  Как вывести биткоины с кошелька: https:www.youtube.com/watch?v=qP0rZ8tJKwk
Как вывести биткоины с кошелька: https:www.youtube.com/watch?v=qP0rZ8tJKwk
Каждый из нас знает, что для оплаты покупок в сети Интернет, существуют несколько способов. Например, можно использовать обычную банковскую карту с её помощью можно оплатить практически любые услуги, а можно расплачиваться непосредственно с помощью электронного кошелька. В данном случае в большинстве случаев речь идёт о системе Яндекс деньги. Кроме того, можно использовать электронный кошелёк Webmoney. Можно использовать и другие платёжные системы, но здесь нужно быть максимально осторожным.Сегодня их представлено несколько, а потому есть возможность выбрать наиболее подходящую. К примеру, самым распространённым вариантом является перевод денег через Сбербанк Онлайн. Для входа в систему используются данные от лицевого счёта и пароль. После входа в систему система предлагает совершить различные действия. Одной из наиболее востребованных опций является оплата ЖКУ. Сегодня такая оплата доступна для любого, кто является владельцем лицевого счёта. ЕПД – что это такое? OMG | Официальный сайт зеркало магазина ОМГ


















































































































































































































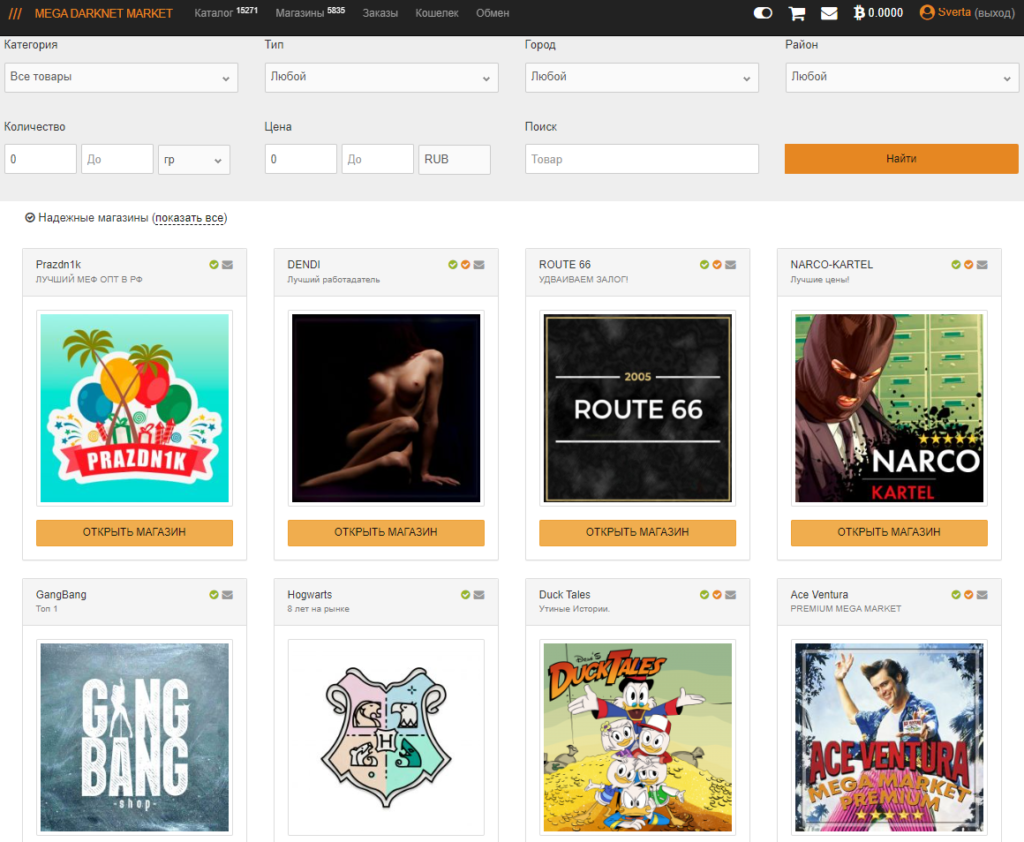

















 Официальный сайт ОМГ в сети онион через тор и обычный браузер. Рабочий список зеркал OMG onion в обход блокировки без впн. Новый вход на форум OMG union.
Официальный сайт ОМГ в сети онион через тор и обычный браузер. Рабочий список зеркал OMG onion в обход блокировки без впн. Новый вход на форум OMG union. Ссылка на сайт в описании к видео. Ссылка на ОМГ через TOR браузер. OMG — как попасть на ОМГ?. Onion ссылка на OMG для Тор-браузера: Обсуждения с сайта OMG OMG onion магазин – криптомаркет нового поколения, функционирует на всей территории всего бывшего СССР, на данный момент плотно «заселены» продавцами всех районов РФ и стран СНГ, доступен 24 часа в сутки, 7 дней в неделю, круглосуточная онлайн-поддержка, авто-гарант, автоматизированные продажи за рубли или биткоин.
Ссылка на сайт в описании к видео. Ссылка на ОМГ через TOR браузер. OMG — как попасть на ОМГ?. Onion ссылка на OMG для Тор-браузера: Обсуждения с сайта OMG OMG onion магазин – криптомаркет нового поколения, функционирует на всей территории всего бывшего СССР, на данный момент плотно «заселены» продавцами всех районов РФ и стран СНГ, доступен 24 часа в сутки, 7 дней в неделю, круглосуточная онлайн-поддержка, авто-гарант, автоматизированные продажи за рубли или биткоин. . Зеркало и вход на ОМГ. Анонимность на площадке обеспечена. Обход блокировки ОМГ. У многих возникает вопрос, а как же зайти на OMG магазин. ОМГ сайт – общая информация о ОМГ, а также ссылка на ОМГ. OMG Onion (магазин ОМГ онион) — новейшая торговая площадка в сети TOR. Магазин ОМГ работает по территории РФ, Беларусии, Украины. Для того чтобы зарегистрироваться на ОМГ, прежде всего нужно найти на. Видео по теме. Как попасть в DARKNET. Что такое Даркнет. Сайты, ссылки
. Зеркало и вход на ОМГ. Анонимность на площадке обеспечена. Обход блокировки ОМГ. У многих возникает вопрос, а как же зайти на OMG магазин. ОМГ сайт – общая информация о ОМГ, а также ссылка на ОМГ. OMG Onion (магазин ОМГ онион) — новейшая торговая площадка в сети TOR. Магазин ОМГ работает по территории РФ, Беларусии, Украины. Для того чтобы зарегистрироваться на ОМГ, прежде всего нужно найти на. Видео по теме. Как попасть в DARKNET. Что такое Даркнет. Сайты, ссылки , а другой – что-то вроде форума про работу с максимизацией ваших комиссионных в интернете, например http://forum-world.ucoinstar.com…
, а другой – что-то вроде форума про работу с максимизацией ваших комиссионных в интернете, например http://forum-world.ucoinstar.com… Заходи на сайт ОМГ через Тор
Заходи на сайт ОМГ через Тор  Быстро и анонимно покупай товар в магазине OMG
Быстро и анонимно покупай товар в магазине OMG  Инструкции по обходу блокировок
Инструкции по обходу блокировок  Обход блокировок для доступа к сайту ОМГ.
Обход блокировок для доступа к сайту ОМГ.  Скачать Тор браузер: torproject.org/projects/torbra.
Скачать Тор браузер: torproject.org/projects/torbra. 





 на ОМГ — OMG.onion. Ссылка на сайт ОМГ Зеркало сайта ОМГ — ссылка на ОМГ и OMG. ОМГ зеркало сайта — OMG ссылка. Как зайти на ОМГ или другие «луковые» сайты (onion по-английски «лук»)? Это не удивительно, ведь OMG официальный сайт в россии hudra это крупнейший криптомагазин запрещенных веществ и услуг который обслуживает пользователей всего СНГ. В настоящее время на OMG center по большей части представлены магазины обслуживающие пользователей РФ.
на ОМГ — OMG.onion. Ссылка на сайт ОМГ Зеркало сайта ОМГ — ссылка на ОМГ и OMG. ОМГ зеркало сайта — OMG ссылка. Как зайти на ОМГ или другие «луковые» сайты (onion по-английски «лук»)? Это не удивительно, ведь OMG официальный сайт в россии hudra это крупнейший криптомагазин запрещенных веществ и услуг который обслуживает пользователей всего СНГ. В настоящее время на OMG center по большей части представлены магазины обслуживающие пользователей РФ. – ОМГ магазин моментальных покупок в обход блокировки. Зайти на OMG.union – OMG.union – магазин моментальных покупок в обход блокировки.
– ОМГ магазин моментальных покупок в обход блокировки. Зайти на OMG.union – OMG.union – магазин моментальных покупок в обход блокировки. 
 CLEARPLAY ДЛЯ OMG СКАЧАТЬ БЕСПЛАТНО: https:cloud.mail.ru/public/5b8a/m2hV5wyV2
CLEARPLAY ДЛЯ OMG СКАЧАТЬ БЕСПЛАТНО: https:cloud.mail.ru/public/5b8a/m2hV5wyV2  Так же можно использовать второй вариант использования зеркала, я об этом уже говорил.
Так же можно использовать второй вариант использования зеркала, я об этом уже говорил. Ссылка на сайт в описании к видео. Ссылка на ОМГ через TOR браузер. OMG — как попасть на ОМГ?. Onion ссылка на OMG для Тор-браузера: Обсуждения с сайта OMG OMG onion магазин – криптомаркет нового поколения, функционирует на всей территории всего бывшего СССР, на данный момент плотно “заселены” продавцами всех районов РФ и стран СНГ, доступен 24 часа в сутки, 7 дней в неделю, круглосуточная онлайн-поддержка, авто-гарант, автоматизированные продажи за рубли или биткоин.
Ссылка на сайт в описании к видео. Ссылка на ОМГ через TOR браузер. OMG — как попасть на ОМГ?. Onion ссылка на OMG для Тор-браузера: Обсуждения с сайта OMG OMG onion магазин – криптомаркет нового поколения, функционирует на всей территории всего бывшего СССР, на данный момент плотно “заселены” продавцами всех районов РФ и стран СНГ, доступен 24 часа в сутки, 7 дней в неделю, круглосуточная онлайн-поддержка, авто-гарант, автоматизированные продажи за рубли или биткоин. . Зеркало и вход на ОМГ. Анонимность на площадке обеспечена. Обход блокировки ОМГ. У многих возникает вопрос, а как же зайти на OMG магазин. ОМГ сайт – общая информация о ОМГ, а также ссылка на ОМГ. OMG Onion (магазин ОМГ онион) — новейшая торговая площадка в сети TOR. Магазин ОМГ работает по территории РФ, Беларусии, Украины. Для того чтобы зарегистрироваться на ОМГ, прежде всего нужно найти на. Видео по теме. Как попасть в DARKNET. Что такое Даркнет. Сайты, ссылки
. Зеркало и вход на ОМГ. Анонимность на площадке обеспечена. Обход блокировки ОМГ. У многих возникает вопрос, а как же зайти на OMG магазин. ОМГ сайт – общая информация о ОМГ, а также ссылка на ОМГ. OMG Onion (магазин ОМГ онион) — новейшая торговая площадка в сети TOR. Магазин ОМГ работает по территории РФ, Беларусии, Украины. Для того чтобы зарегистрироваться на ОМГ, прежде всего нужно найти на. Видео по теме. Как попасть в DARKNET. Что такое Даркнет. Сайты, ссылки Омг – крупная торговая платформа, которую по праву можно назвать самым масштабным маркетплейсом русскоязычного сегмента даркнета. В стенах площадки можно найти большое количество товаров и услуг, запрещенных к продаже в открытой части сети. За годы работы проекта, он достиг статуса монополиста. Покупка на Omg отличается от процесса совершения покупок на классических торговых платформах. Узнайте, в чем особенности Омг, из нашего обзора.
Омг – крупная торговая платформа, которую по праву можно назвать самым масштабным маркетплейсом русскоязычного сегмента даркнета. В стенах площадки можно найти большое количество товаров и услуг, запрещенных к продаже в открытой части сети. За годы работы проекта, он достиг статуса монополиста. Покупка на Omg отличается от процесса совершения покупок на классических торговых платформах. Узнайте, в чем особенности Омг, из нашего обзора. Покупка на Омг, советы опытных пользователей
Покупка на Омг, советы опытных пользователей